| Термин | Определение |
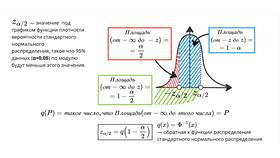
| Доверительный уровень | Вероятность, с которой интервал содержит истинный параметр (обычно 90%, 95% или 99%) |
| Точечная оценка | Выборочная статистика, используемая для оценки параметра |
| Предельная ошибка | Половина ширины доверительного интервала |
- Среднее значение
- Доля
- Разность средних
- Коэффициент регрессии
- Определите необходимый уровень надежности (обычно 95%)
- Найдите соответствующее критическое значение z или t
- Для нормального распределения используйте z-статистику
- Для малых выборок (n < 30) применяйте t-распределение
| Параметр | Формула стандартной ошибки |
| Среднее | SE = σ/√n (σ - стандартное отклонение) |
| Доля | SE = √(p(1-p)/n) |
| Разность средних | SE = √(σ₁²/n₁ + σ₂²/n₂) |
- При известном σ: x̄ ± z*(σ/√n)
- При неизвестном σ: x̄ ± t*(s/√n)
- Для малых выборок: коррекция на (n-1) степеней свободы
- p̂ ± z*√(p̂(1-p̂)/n)
- Для малых выборок используйте поправку на непрерывность
- При p близких к 0 или 1 применяйте специальные методы
| Шаг | Действие |
| 1 | Выборка: n=100, x̄=50, s=10 |
| 2 | Доверительный уровень 95% → z=1.96 |
| 3 | SE = 10/√100 = 1 |
| 4 | Предельная ошибка = 1.96*1 = 1.96 |
| 5 | Доверительный интервал: 50 ± 1.96 → (48.04, 51.96) |
- R: t.test() или prop.test()
- Python: scipy.stats.norm.interval()
- SPSS: Анализ → Описательные статистики → Исследовать
- Excel: ДОВЕРИТ.НОРМ() или ДОВЕРИТ.СТЬЮДЕНТ()
- Ширина интервала зависит от объема выборки и изменчивости данных
- Более высокий доверительный уровень дает более широкий интервал
- Доверительный интервал не означает вероятность для параметра
- Перекрытие интервалов не всегда свидетельствует о незначимости различий
- Использование z-статистики вместо t для малых выборок
- Неучет поправок для пропорций близких к 0 или 1
- Интерпретация доверительного интервала как области значений выборки
- Игнорирование предположений о нормальности распределения
Важные замечания
При построении доверительных интервалов для сложных статистик (медианы, коэффициентов регрессии) могут потребоваться специальные методы, такие как бутстреп. Для непараметрических данных следует использовать методы, не зависящие от предположения о нормальности распределения.